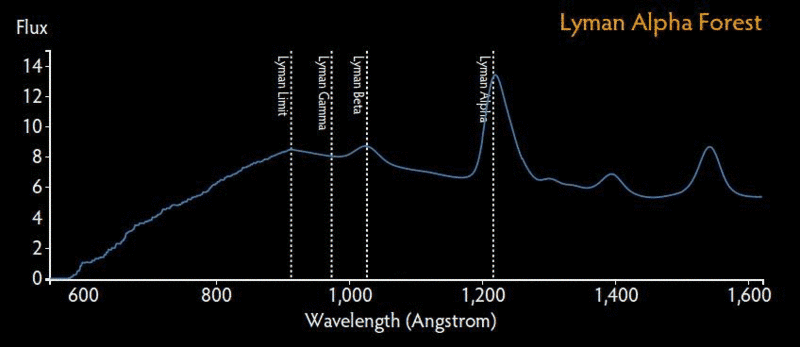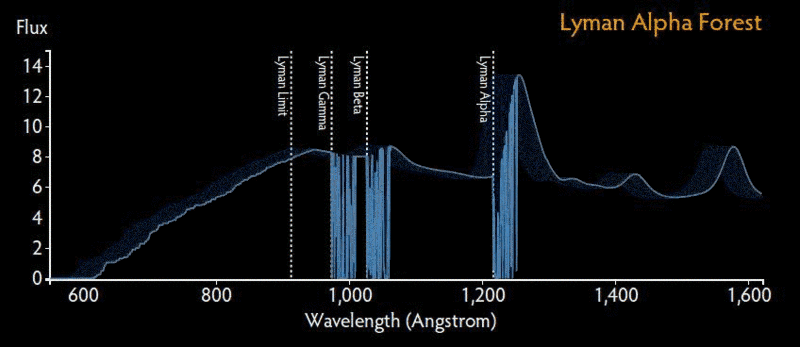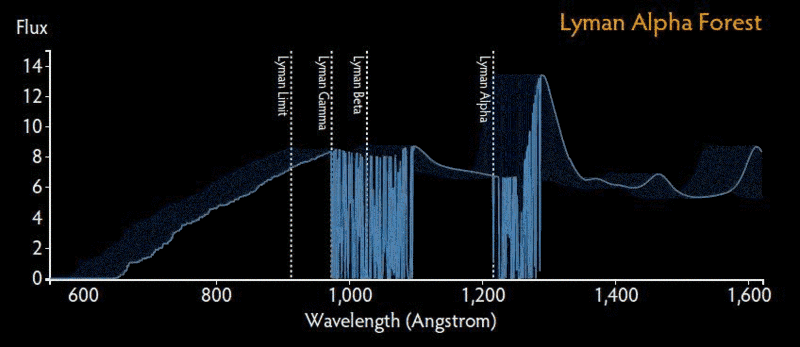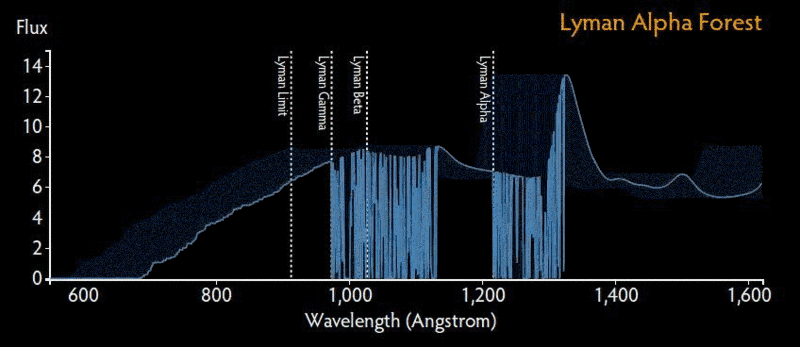
Image credit: Yuan-Sen Ting , CC BY-SA 4.0 via Wikimedia Commons.
Overview
This is a one year project funded by the European Commission Horizon 2020 Marie Skłodowska-Curie Actions Cofund program “Co-Funded Brain Circulation2 Scheme (CoCirculation2)” introduced by the Turkish Scientific and Technological Research Council (TÜBİTAK).
Motivation behind the project
When we look deep into the Universe with powerful telescopes and analyze the data that we have received, we come to the realization that we can explain only 5% of the energy content in the observable universe1. The rest of it is postulated to consist of dark matter and dark energy. Understanding these substances remains to be one of the biggest challenges of today’s High Energy Physics and Cosmology.
Even though dark energy remains to be a big mystery, we have strong clues about what properties dark matter should have. These can be summarized under the so-called Cold Dark Matter (CDM) hypothesis. Even though this is the model which fits the cosmological data best2, it faces some difficulties when it is confronted with the observations of small-scale structures. In these scales, the results of numerical simulations of CDM do not align with what we observe in the universe. In the literature, this is known as the “small-scale crisis of CDM”3.
One way to solve the small-scale crises of CDM is to modify the CDM hypothesis. A popular candidate for this is the Fuzzy Dark Matter (FDM), also known in the literature as Ultra Light Dark Matter (ULDM), or Ultra Light Axions (ULA)4. This model is very similar to CDM, except its dark matter particle is extremely light. It has been claimed that an FDM of mass on the order of 10-22 eV (electron volts) might provide a solution to the small-scale crisis of CDM5.
There is still one catch though. In simple models of FDM where the potential for the dark matter particle can be approximated by a quadratic one, which means that the dark matter can be considered as a free particle without any interactions, FDM does an excessively good job in eliminating structure on small scales so that it is in conflict with some observations, most notably with the observations of Lyman-α forest. If one compares the power spectrum obtained from these observations with the one predicted by the FDM model with a quadratic potential, one can put a strong bound on the FDM mass on the order of 10-20 eV which renders the FDM solution to the small scale crisis not viable6.
The situation is not as clear when one considers slightly more complicated potentials for FDM, in other words, if one goes beyond the free particle approximation. It has been claimed that taking into account the self-interactions of FDM particles, even if they are extremely tiny, can change the Lyman-α results drastically7. Also, it has been found that in models containing a mechanism that enhances the power spectrum at certain scales the resulting enhancement can make the FDM model with a mass of 10-22 eV consistent with the Lyman-α data8. These works provide a strong motivation for careful studies of various FDM models in light of the Lyman-α data.
Goals of the project
My primary goal in this project is to study the impact of FDM self-interactions on the Lyman-α observations. In particular, I want to find out whether the inclusion of self-interactions weakens of strenghtens the bound on the FDM particle mass put by the Lyman-α observations.
References
Planck Collaboration et al, 2020, Astron Astrophys 641: A6. ↩︎
Heavens et al, 2017, Phys Rev Lett 119: 101301. ↩︎
Weinberg et al, 2015, Proc Natl Acad Sci 112: 12249–55. ↩︎
Sahni & Wang, 2000, Phys Rev D 62: 103517; Peebles, 2000, Astrophys J 534: L127; Hu et al, 2000, Phys Rev Lett 85: 1158–61; Press et al, 1990, Phys Rev Lett 64: 1084–87. ↩︎
Walker & Peñarrubia, 2011, ApJ 742: 20; Lora et al, 2012, J Cosmol Astropart Phys 2012: 011–011; Schive et al, 2014, Nat Phys 10: 496–99. ↩︎
Rogers & Peiris, 2021, Phys Rev Lett 126: 071302. ↩︎
Desjacques et al, 2018, Phys Rev D 97: 023529. ↩︎
Leong et al, 2019, Mon Not R Astron Soc 484: 4273–86. ↩︎